I Built an Erdős-Rényi Graph Generator
How to generate random graphs, and why it's important in analyzing biological transcription networks (as well as other kinds of networks)
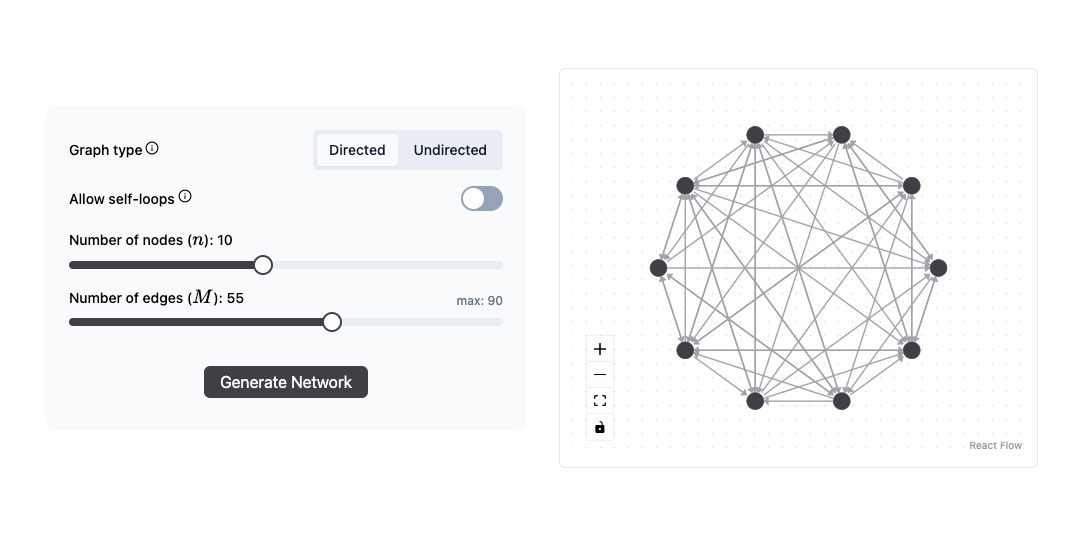
TL;DR: I made an Erdős-Rényi random graph generator, which you can check out here on Newt Interactive. Below is a short screen recording showing how it works. The website also has a short intro to what Erdős-Rényi graphs are, which I’ll also talk about in this post, as well as some of the reasons I made it.
While reading the Chapter 2 in An Introduction to Systems Biology, I learned about the concept of network motifs, which is a pattern in a network that occurs much more often than would at random. In transportation networks, a network motif could be the emergence of hubs — single locations that connect to and from a lot of other locations. In biological transcription networks, a network motif could be the emergence of master regulatory transcription factors — single proteins that play a role in regulating a lot of other genes. Or it could be the discovery of autoregulation — transcription factors that regulate themselves — which is what the chapter in the book explores.
Regardless of the application, in order to know that something occurs much more than at random, it needs to be compared to the random. Given that we have a real network, how can we compare it to a random one?
A simple model of random networks was created by Hungarian mathematicians Paul Erdős and Alfréd Rényi, called the Erdős-Rényi (ER) model. The model comes in two variants: G(n,p) and G(n,M).
With G(n,p), you start with n number of nodes and then connect each pair of nodes (create an edge between them) with a probability p, independent of all other pairs. If the probability is 1, all nodes will be connected. If it’s 0, none will be connected. If it’s 0.5, then whether a connection is made is like tossing a coin.
With G(n,M), you start with n number of nodes and randomly select M edges (from all possible edges) to connect the nodes. This is a useful method for generating graphs when you want a specific number of edges.
The generator I built is for the G(n,M) variant. If you liked it and would like to play with the G(n,p) one as well, or have any other questions, please comment or reach out to me!
Building this model from scratch taught me a lot of details about how it works; the process made me ask a lot of questions about what steps were right, details that I did not consider after just reading about it. The graph generator is a stepping stone in working on my interactive Systems Biology series. In an upcoming article on autoregulation, you will see how real networks are compared to random ones, and how by using this comparison we can find that autoregulation is a network motif in biological transcription networks, and what advantages that might hold for organisms. If you’re interested in this topic, you can start with Part One: Transcription Network Basics, or check out the whole series (so far)!