Simulating the Evolution of Genetic Circuits: Part One
I built a simulator that shows you genetic circuit evolution step-by-step
If you’d like to jump straight to the simulator, here’s the link. Read on for some context, notes, and future ideas.
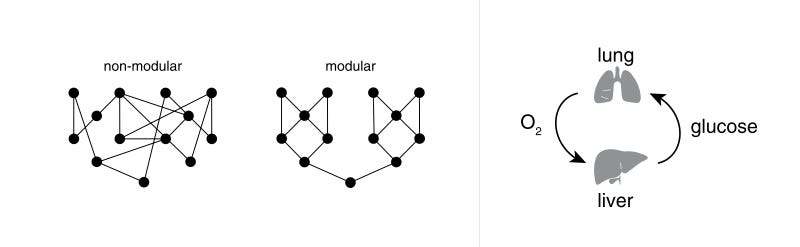
In Part Three of An Introduction to Systems Biology, Uri Alon introduces the concept of modularity in biological networks. A modular system is one that can be broken down into smaller, independent components that each have a specific function. The simplest analogy is LEGO: large, elaborate structures can be built from a small group of blocks. If some of your blocks go missing — accidentally vacuumed and thrown out, lost to another dimension after rolling under the couch — you can simply get identical ones, and continue building with doing a lot of re-working. Another example is cars: batteries, transmissions, motors, tires, etc. can be easily replaced without taking the entire vehicle apart.
Organisms tend to show similar modularity in their structures at all levels. At the organ level, Alon provides the example of our lung and liver. The liver supplies glucose and blood proteins to the body, the lung supplies oxygen and removes CO2; the liver needs the lung’s oxygen to function, the lung needs the liver’s glucose to function. You could, theoretically, replace the lung with something that matches its output, and the liver will continue to function (like with a heart-lung machine temporarily, for example). They’re modules in the larger system, our body.
A similar structure is also found in the cellular level: each cell has subparts, like the nucleus, ribosome, etc. that have their own function. And it’s also found at the level of proteins, with sub-structures like different binding and dimerization sites.
LEGOs and cars are engineered to be that way: modularity is beneficial for cost-saving and mass-manufacturing, for instance. Biology. however, didn’t have an MBA graduate and factory engineer pore over best practices. So, why did it evolve modularity as well?
To begin answering this question, Alon described some results of computer simulations. He reported that, in simple computer simulations of evolution, non-modularity is the norm. He writes:
In evolutionary simulations, a population of networks is evolved by randomly adding, removing and changing connections between nodes – and even duplicating and recombining parts of the networks – until the networks perform a given computation goal, that is, until the networks give the correct output-to-input relationship.
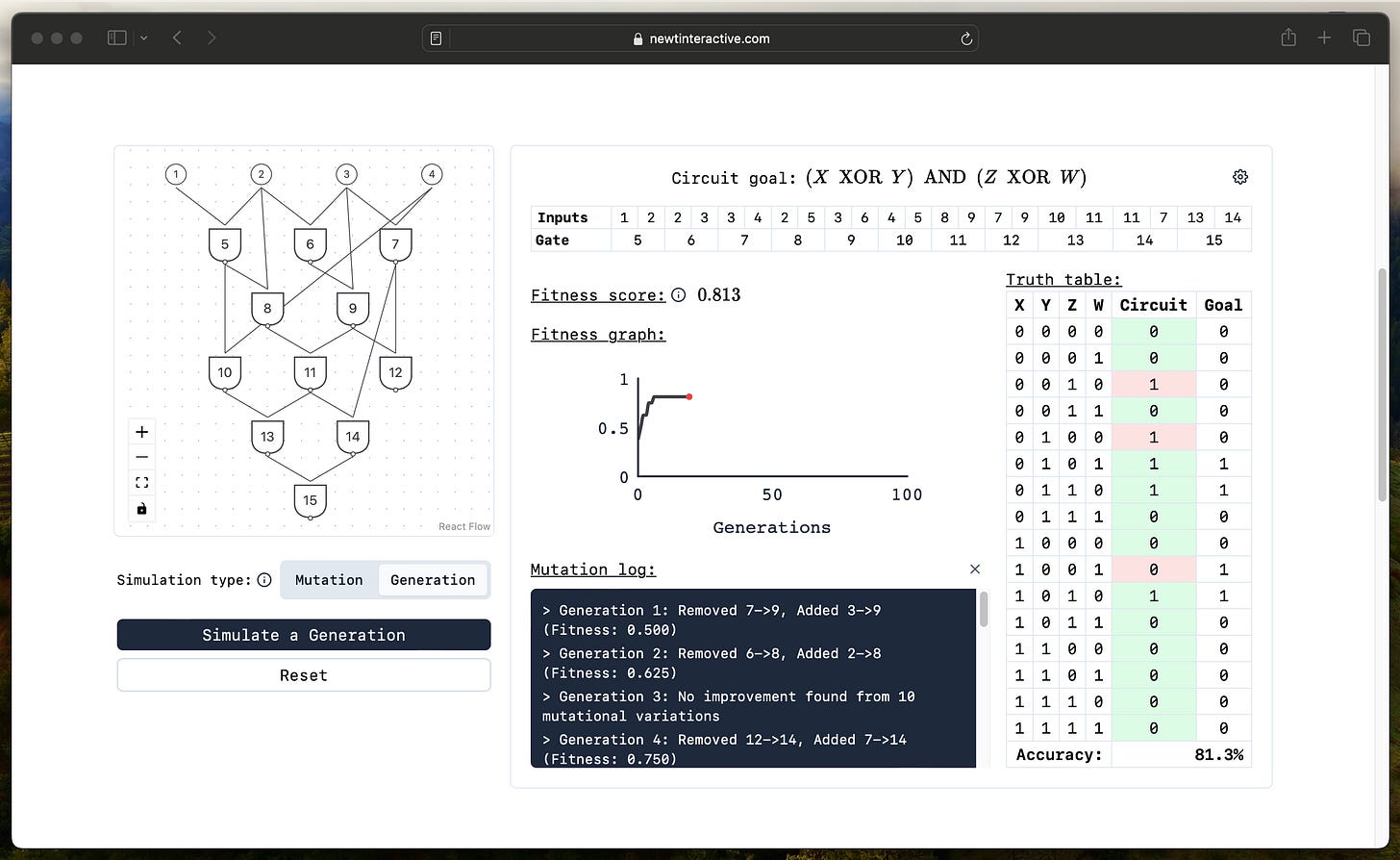
He specifically goes on to describe a network of NAND gates, and mutations that changed the network. I thought this sounded really interesting, so I decided to create a simple computer simulation that does some of this and see how a network “evolves” myself. You can check it out on my website, Newt Interactive! I recommend playing around with it first and getting a feel for what’s going on and noticing some patterns.
This simulator comes in two modes: Mutation and Generation. In Mutation, you simulate a random change to the circuit — in this case, it’s just changing the connections. In Generation mode, N variants of the circuit are simulated, each with a single mutation, and from these variants (and the original) the highest scoring circuit is selected. This is a rough mimicry of natural selection, and shows different behavior compared to just random mutations.
If you try out the Generation simulation, you’ll see the same phenomenon that Alon goes on to discuss in the chapter: logarithmic slowdown. Essentially, the circuit quickly improves at first, and then hits a wall and stays at the same spot for a long time. (Mine’s capped to 100 generations for now, but usually getting to the perfect score takes around 10,000 generations).
Why make this
I wanted to build this for a few reasons:
as I was reading the chapter, I wanted to visually see the changes per mutation/generation (and what happens when I change parameters)
the process of building something usually brings a deeper understanding of the problem, as well as coming to the same insights but through first-principles
it’s a stepping-stone to build more complex simulations, like the one required to see modularity evolve, which I’ll explore in a future Part Two post.
Modularity and Simulator 2.0
The reason these simulations evolve into non-modularity is because it’s the most efficient, but often networks get stuck in local maxima that delay reaching that perfect solution — the logarithmic slowdown. As Alon reveals later in the chapter, modularity is achieved by evolution when the goal varies periodically, as long as both those goals tend towards the same direction; in other words, two goals where working on one gets you closer to the other. In short, this change provides an opportunity for circuits to exit local maxima without veering too far from either goal.
In simulations, this is done with circuits and varying logic goals, and the results are explored in detail at the end of the chapter in the book. Modular solutions are less efficient (in this case, the modular one requires 11 nodes, versus the 10 for the non-modular one), but reach their goal faster.
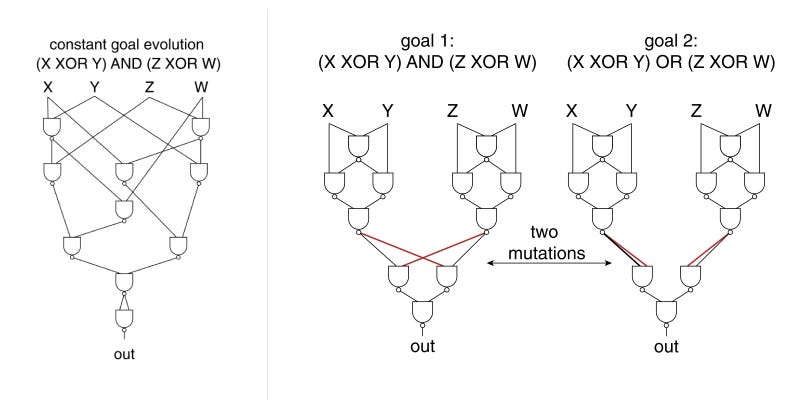
My goal here is to make this part of the simulation as well. Like with the above version, I’d like to see the changes as they happen and watch “evolution” reach modularity. This requires some upgrades to the circuit simulation I have, which I’ll roughly list here, but will build in the future and explore more deeply in Part Two:
mutations should include ability to add/remove nodes (right now only changes connections)
more variations created per generation (right now capped to 20)
up to 10,000 generations (right now capped to 100)
ability to skip ahead some number of generations (having to click 10,000 times would be pretty painful)
switching circuit goals (either manually, or automatically for modularly varying goals)
automatic visual reorganizing of circuits (right now it can get quite messy, although I’m not quite sure how to do this)
measuring modularity (there are algorithms that do this)
other visual indicators, like the mountain climbing visual in the book?
Of course, as I build it, other ideas will come forth or some of these might not seem that great (or impractical). But should be interesting.
If you find this interesting as well, or have any feedback/questions or find any issues with the simulator, I’d love to hear from you!