Simulating Genetic Circuits: Biological AND Gates

I built a simulator that shows you how the coherent type-1 feed-forward loop, a biological AND gate, works

If you’d like to jump straight to the simulator, here’s the link. Read on for some context, notes, and future ideas.

---

In my previous post, I wrote about the simulator I built to explain how genetic circuits evolve through random mutations. This time, let’s explore a specific type of genetic circuit — the coherent type-1 feed-forward loop — which I first learned about in Chapter 3 of An Introduction to Systems Biology.

Feed-forward loops (FFLs) are among the most common network motifs in biology — recurring patterns that show up far more often than you’d expect by chance. In a feed-forward loop, a transcription factor X regulates a second transcription factor Y, both of which regulate gene Z. So there are two paths to activation for Z, a direct path (X) and a delayed path through an intermediate (Y).

There are 8 types of FFLs, which can be split into two groups: coherent and incoherent. In coherent FFLs the indirect path (X → Y → Z) has the same sign (positive or negative) as the direct path (X → Z). In incoherent FFLs, the signs are opposite. The diagram below shows all the combinations:

The 8 types of feed-forward loops (3 nodes). The flat-headed arrow represents repression, or a negative sign.

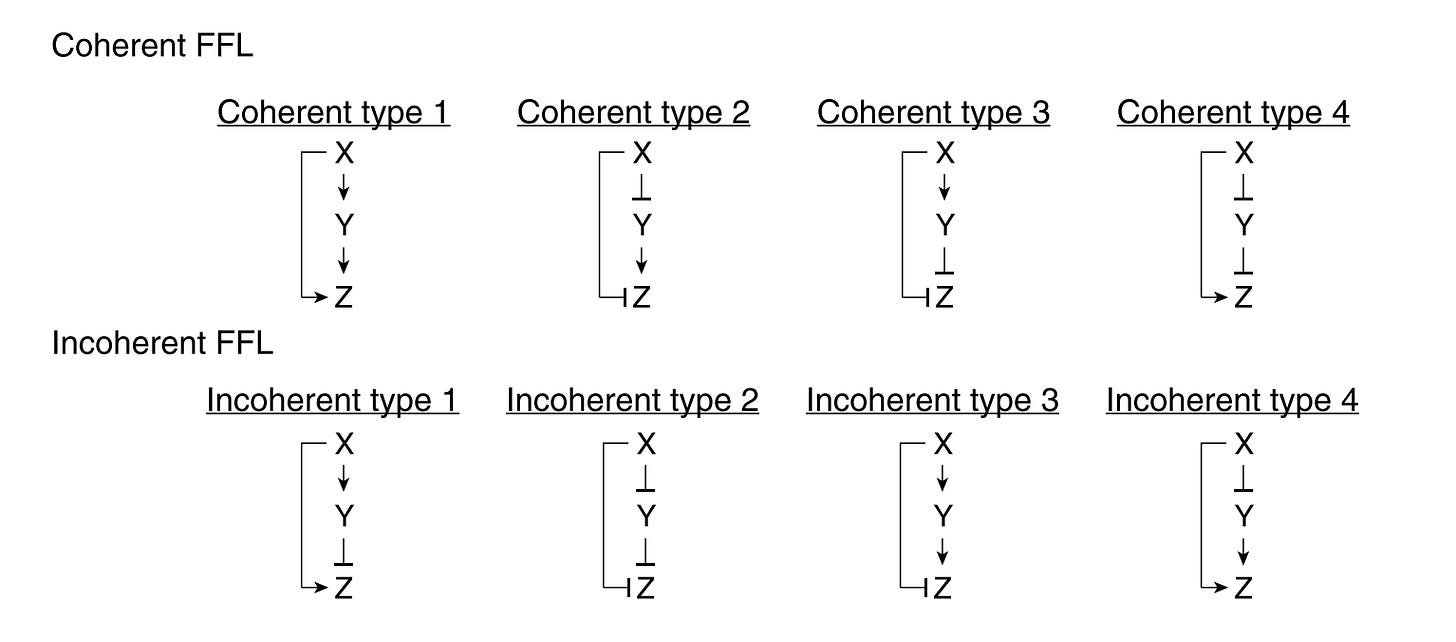
The specific one I built a simulator for is the coherent type-1 feed-forward loop (C1-FFL), where both paths are activators. You can think of this like so: imagine you're at a company with a particularly bureaucratic approval process. To achieve your goal of geting a project approved by the VP (Z), you need sign-off from both your direct manager (X) and the department head (Y). Once you submit your project (the signal), your manager approves really quickly, but the department head is busy and takes longer to approve, before reaching the VP’s desk.

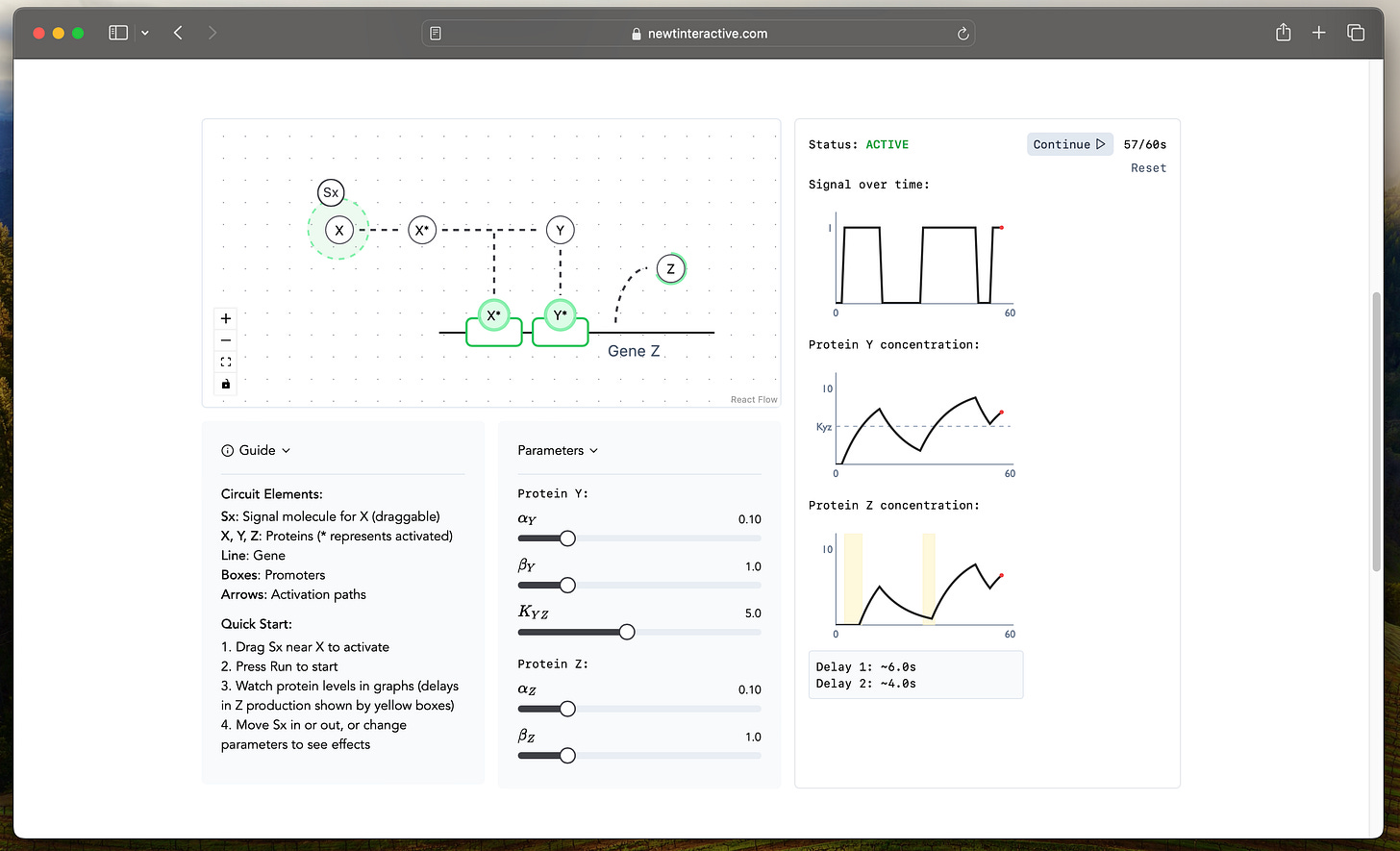
This is exactly how a C1-FFL works in biology. When a signal (Sx) comes in, it activates both a fast-responding transcription factor (X), which in turn activates the intermediate transcription factor (Y), both of which regulate the target gene (Z). If you’re familiar with some programming, this essentially functions as a biological AND gate. This architecture encodes some interesting behaviours, and I built a simulator to play with and explore exactly this. I encourage you to check it out before reading the details of the behaviours below.

Circuit Behavior

In the chapter, Uri Alon describes the two behaviours this type of circuit generates: a sign-sensitive delay and persistence detection. You can visualize these through the simulation. Sign-sensitive delay refers to the fact that starting the production of Z has a delay (shown by yellow boxes in the screenshot below) because it depends on both X and Y, but stopping production, after either of the two transcription factors is removed, does not. This delay works as a persistence detector for ON pulses: Z only responds if there is a persistent signal from X AND Y; or, in other words, it is filters out noise in the system.

Coherent Type-1 Feed-forward Loop Simulator on Newt Interactive. Delays are represented with yellow boxes. And you can change parameters and see how that affects the charts/simulation runs.

The Arabinose system in E.Coli

A great example of C1-FFL in action is the Arabinose system of E.Coli. Alon explains the whole thing in a lot more experimental detail in Chapter 3, so I encourage you to check it out there, but I’ll briefly summarize it here.

Arabinose is a sugar, but it’s only used by most cells if glucose is not present as glucose is a far better energy source and arabinose is costlier to digest. So, E.Coli only wants to build the machinery to digest arabinose if glucose is not present and arabinose is. The absence of glucose is represented by a small molecule called cAMP, which is the signal that activates the transcription factor CRP (let’s call this X from our example). Another transcription factor, AraC, senses arabinose (this can be Y). These two regulators are part of the system to produce arabinose utilization proteins araBAD and araFGH.

Experiments show that there’s a delay in producing the final proteins compared to simple regulation when both signals are ON, but no delay when stopping protein production. This is incredibly useful when there’s a huge cost associated with building particular proteins for a cell, which in this case is the arabinose utilization proteins. This circuit design enables E.Coli to only produce them when they’re absolutely certain that they are necessary (persistence detection), and immediately stop expensive production as soon as a better option is available (in this case, the appearance of glucose and so disappearance of cAMP.

Future Ideas

I hope that this simulator allows you to play with this incredibly cool facet of life, and try different parameters and see what happens. It’s the first in this specific kind of interactive circuit simulation I’ve always wanted to make. Every time I learn about a concept like this, I wish that I could visualize it in real-time, change some parameters, and see what happens. They’re also fun to make and I learn a lot in the process.

I can also use this as the foundation to build similar simulators for other circuit designs with other features, like incoherent type-1 FFLs (speed up ON and biphasic response), single-input modules (temporal expression, just-in-time production), positive autoregulation (bistability), and many more.

It also sets up a future interactive I would like to build, where you can drag-and-drop to create and run your own genetic circuit. This step brings that goal a little closer.

If you find this interesting as well, or have any feedback/questions or find any issues with the simulator, I’d love to hear from you! Otherwise, thanks for checking this out, and I’ll see you in the new year!